Lumbar puncture needle length determination
Original Contribution
Lumbar puncture needle length determination

Keith K. Abe MD, MSa, Loren G. Yamamoto MD, MPH, MBAa,b,*, Erick M. Itoman MDa,b,
Terri A.F. Nakasone RNb, Stacy K. Kanayama MDb
aDepartment of Pediatrics, University of Hawaii John A. Burns School of Medicine, Honolulu, HI 96826, USA
bEmergency Department, Kapiolani Medical Center For Women And Children, Honolulu, HI 96826, USA
Received 18 February 2005; accepted 5 March 2005
Abstract
Introduction: Appropriate lumbar puncture needle length selection may be more difficult for less experienced practitioners or for patients who are of unusually large or small body habitus. The purpose of this study is to determine if there is a relationship between body height and weight, and the percutaneous depth to the Spinal canal, which can more reliably assist in selecting an LP needle length. Methods: This is a retrospective cohort study of patients who received an abdominal computed tomographic scan (for any reason) from July 1999 to December 2000. Lumbar puncture depth was measured on the computed tomographic scan and was used to derive a formula.
Results: The final data pool consisted of 175 patients, aged 25 days to 80 years, with height of 48 to
181.5 cm, weight of 3.0 to 127.3 kg, and body mass index of 11.7 to 49.7 kg/m2. Using this data set, the formula for predicting the required LP depth is (weight in kilograms, height in centimeters):
LP depth (cm)= 1 + 17 x
weight
.
height
Using linear regression comparing the skin to mid-spinal canal depth measurements with the calculated LP depths, R2 was 0.81 ( P b.001). This formula selected a needle that was too short in 6% (less than that of 4 other previously published LP needle length selection methods) and a needle that was too long in 31%. Conclusion: Compared with other formulas, this formula might be a more reliable predictor for estimating the required LP needle length, but this must be validated by further studies. It should be noted that none of the formulas were perfect.
D 2005
Introduction
lumbar puncture is a common procedure performed in the diagnostic evaluation of patients at risk
T Corresponding author. Department of Pediatrics, University of Hawaii John A. Burns School of Medicine, Honolulu, HI 96826, USA. Tel.: +1 808 983 8387; fax: +1 808 945 1570.
E-mail address: [email protected] (L.G. Yamamoto).
for meningitis, encephalitis, subarachnoid hemorrhage, and other neurologic conditions. Lumbar puncture is also performed therapeutically in some instances. Standard LP needles come in 1.5, 2.5, 3.5 and 5.0 inch lengths (3.8,
6.4, 8.9, and 12.7 cm, respectively). Selection of LP needle length is typically based on experience; however, an unusually obese or cachectic patient may pose more of a challenge. Appropriate LP needle selection may be more difficult for less experienced practitioners or
0735-6757/$ - see front matter D 2005 doi:10.1016/j.ajem.2005.03.012
for patients who are of unusually large or small body habitus.
For example, which LP needle length would be most appropriate for a 15-year-old, 110-kg, 168-cm man who presents to the ED with short-onset fever, headache, and Nuchal rigidity?
In searching for published recommendations on LP needle length selection, 4 references were identified [1-4]. Bonadio et al [1] described 158 children aged 1 to 18 years. They derived a formula based on body surface area (BSA):
Depth of LP (cm)= 0.77 cm + 2.56 x BSA m2 .
Craig et al [2] described 107 children aged 0 to 16 years.
They derived a formula based on height alone: LP depth (cm)= height (cm)x 0.03.
Hasan [3] described 586 children (age range not specified). He derived a formula based on weight alone:
Epidural depth (cm)= 0.8 + 0.05 x weight (kg).
Henretig and King [4] published a textbook recommen- dation as an empirical estimate of LP needle length provided as a function of age. For premature infants and term newborns to 2-year-old children, 1.5-in needles are recom- mended. For children aged 3 to 12 years, 2.5-in needles are recommended. For those older than 12 years, 3.5-in needles are recommended. A footnote that blarger needles may be required depending on patient habitusQ was included.
The purpose of this study is to determine if there is a relationship between body height and weight and the percutaneous depth to the spinal canal, which can more reliably assist in selecting an LP needle length.
Methods
This is a retrospective cohort study of patients who received an abdominal computed tomographic (CT) scan (for any reason) from July 1999 to December 2000. The CT scans were reviewed, and at the level of the Iliac crest, the following distances were measured as noted in Fig. 1:
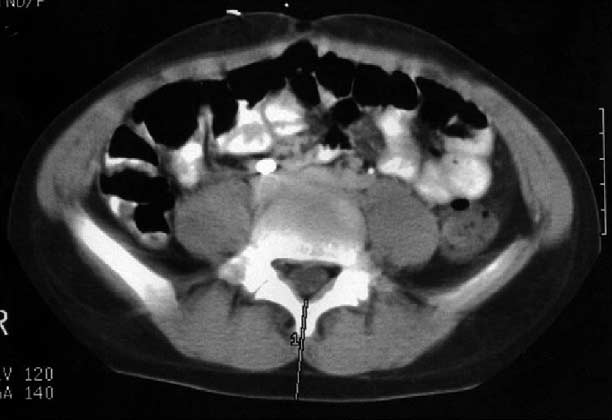
Depth to ant. canal
Depth to post. canal
Fig. 1 Measurements obtained on each CT scan.
16
14


Abe Formula Estimated LP Depth (cm)
12
10
8
6
4
2
0
0 2 4 6 8 10 12 14 16
Measured LP Depth on CT (cm)
Fig. 2 Scattergram of actual LP depths on CT vs Abe formula- estimated depths (linear regression of data points).
(1) skin overlying the spine to the posterior margin of the spinal canal (depth to posterior canal) and (2) posterior to anterior margin of the spinal canal (depth of spinal canal). Age, sex, height, and weight were recorded from the CT and medical records. Those who did not have a height and weight documented on their chart within 3 days of the CT
were excluded.
Lumbar puncture depth was defined as the distance from the skin at the midline of the back to the center of the spinal canal (ie, the depth to the posterior canal + half the depth of the spinal canal). Relationships to patient height and weight (eg, height/weight, height/weight2, [height/weight]2, [height/weight]3), as well as established parameters noted previously (BSA, height, weight, and age), were studied by regression analysis. The best predictive formula for mea- sured LP depths was thus derived.
The predictive formulas from the studies mentioned previously were then compared with the formula derived in this study. Patient body parameters were used to estimate a predicted needle length, and this was compared with the distance measured on CT. The predicted needle length was considered btoo short Q if the needle would be unable to reach the spinal canal based on CT measurements. The predicted needle length was considered btoo long Q if a shorter needle, which would have reached the spinal canal, could have been used. The results for each of the different predictive formulas were compared.
Results
The final data pool consisted of 175 patients aged 25 days to 80 years (median, 16 years; mean, 20.0 F 15.2 years). Height ranged from 48 to 181.5 cm (median, 153.5 cm; mean, 143.8 F 28.4 cm). Weight ranged from 3.0 to
|
set ( P b .001) |
|||
|
Abe et al (wt/ht) |
0.81 |
b.001 |
0.81 |
|
Bonadio et al [1] (BSA) |
0.93 |
N/A |
0.74 |
|
Craig et al [2] (ht) |
N/A |
N/A |
0.48 |
|
Hasan [3] (wt) |
0.8 |
b.01 |
0.79 |
|
Henretig and King [4] |
N/A |
N/A |
0.45a |
|
0-1 |
1-4 |
5-12 |
13-21 N21 |
||
|
Abe et al |
175 |
7 |
12 |
51 |
42 63 |
|
Bonadio et al [1] |
158 |
102 |
40 |
16 (N36 |
mo) |
127.3 kg (median, 52.7 kg; mean, 51.3 F 26.2 kg). Body mass index (BMI) ranged from 11.7 to 49.7 kg/m2 (median, 21.2 kg/m2; mean, 22.6 F 7.2 kg/m2).
Table 1 Comparison of R2 values published from their original data sets
R2
P
Calculated R2
Linear regression compares the calculated needle depth with the measured (on CT scan) needle depth from the skin to the center of the spinal canal. wt indicates weight; ht, height; N/A, not available.
a The decision rule of Henretig and King [4] results in LP needle lengths only and not the depth to the spinal canal. Thus, only values of 1.5, 2.5, and 3.5 in are possible. This will artificially reduce the calculated R2 value.
Table 3 age distribution of LP needle length determination
study groups
Study n Age (y)
107
586
76 10 11
10
No age distribution given
Henretig and King [4] No age distribution given (empirical)
a These numbers are estimates. In the study, no age distribution was given, but the age distribution can be estimated based on the average age for height on standard growth charts.
Using this data set, the formula for predicting the required LP depth is (weight in kilograms, height in centimeters)
weight
LP depth (cm)= 1 + 17 x .
height
This will be referred to as the Abe (pronounced ah-beh) formula during this report to distinguish this from the formula described by other study authors. To obtain the depth in inches (since LP needle lengths come in inch length values), this value should be divided by 2.54 cm/in. Using linear regression comparing the skin to mid-spinal canal depth measurements with the calculated LP depths, R2 was 0.81 ( P b .001) (Fig. 2). Table 1 compares the R2 values of the different LP needle length determination methods, pub- lished from their original data sets, and the newly calculated R2 values using this current data set. The formulas of Bonadio et al [1] and Hasan [3] have high R2 values as well. When the other LP needle length determination methods were compared with the Abe formula using the height,
Table 2 Frequency of selecting LP needles that are too short or too long using LP depth data from this data set
Abe Bonadio Craig Hasan [3] et al [1] et al [2]
|
2-5 y (n = 18) |
||||
|
Henretig Too short 0 |
6 (33) |
6 (33) |
6 (33) |
0 |
|
and Too long 6 (33) King [4] 6-12 y (n = 41) |
0 |
0 |
0 |
9 (50) |
weight, and LP depth measurements from the current data set, the frequency of selecting needles that are too short or too long was determined and tabulated in Table 2. The other LP needle length determination methods had high frequen- cies of selecting LP needle lengths that were too short. The Abe formula had the lowest number of needles that were too short. However, 31% of the time, the Abe formula selected a needle that was too long.
The age distribution for the 2 other studies for which the age distribution is provided [1,2] (see Table 3) consisted mostly of infants (65% [1] in one study and 71% [2] in the other study). The other 2 studies did not provide an age distribution of their patient study group. Our study had a much broader age representation. Table 4 stratifies needle selection miss rates (too short or too long) by age groups. This shows that the Abe formula still has the lowest rates of avoiding needles that are too short in all age groups.
Table 4 Frequency of selecting LP needles that are too short
or too long using LP depth data (using the midpoint of the spinal canal) stratified by age groups
Abe Bonadio Craig
Hasan [3] Henretig
and King [4]
0-24 mo (n = 11)
Too short 0 1 (9) 1 (9) 1 (9) 1 (9)
Too long 0 0 0 0 0
|
the length |
Too short 1 (2) |
17 (42) |
12 (29) |
24 (59) |
10 (24) |
||
|
barely reaches the dural sac) |
Too long 18 (44) |
0 |
7 (17) |
0 |
17 (42) |
||
|
Too short 1 (1) 54 (31) 53 (30) 96 (55) |
13 (7) |
13-18 y (n = 33) |
|||||
|
Too long 97 (55) 5 (3) 15 (9) 1 (1) |
95 (54) |
Too short 2 (6) |
16 (48) |
15 (45) |
29 (88) |
4 (12) |
|
|
Using midpoint of spinal canal (end of the length the middle of the dural sac) Too short 11 (6) 92 (53) 87 (50) 125 (71) |
ends up in 32 (18) |
Too long 15 (45) z19 y (n = 72) Too short 8 (11) |
0 52 (72) |
0 53 (74) |
0 65 (90) |
18 (55) 16 (22) |
|
|
Too long 54 (31) 0 7 (4) 0 |
64 (37) |
Too long 18 (25) |
0 |
0 |
0 |
19 (26) |
|
|
Values are presented as n (%). |
Values are presented as n (%). |
||||||
|
Too short 2 (3) |
15 (21) |
10 (14) |
33 (45) |
0 |
|
Too long 25 (34) 20-30 kg/m2 (n = 81) |
0 |
7 (10) |
0 |
42 (58) |
|
Too short 6 (7) |
58 (72) |
57 (70) |
73 (90) |
16 (20) |
|
Too long 25 (31) N30 kg/m2 (n = 21) |
0 |
0 |
0 |
20 (25) |
|
Too short 3 (14) |
19 (90) |
20 (95) |
19 (90) |
15 (71) |
|
Too long 7 (33) |
0 |
0 |
0 |
1 (5) |
Table 5 stratifies needle selection miss rates by BMI groups to determine if the miss rates are particularly higher in one of these groups. Needles that were too short were selected by all formulas at greater frequencies in the more obese group. The Abe formula selected a needle that was too short in 14%, compared with 90%, 95%, 90%, and 71% for the obese patients (BMI, N30 kg/m2).
Table 5 Frequency of selecting LP needles that are too short
or too long using LP depth data (using the midpoint of the spinal canal) stratified by BMI groups
Abe Bonadio Craig Hasan [3] Henretig et al [1] et al [2] and
King [4]
Values are presented as n (%).
Discussion
The selection of an appropriate LP needle length for a patient is often based upon a physician’s previous experi- ence. Such a valuable judgment tool, however, is lacking in physicians who have not done many LPs. Also, this experience is probably not applicable to patients of unusual body habitus. Accurate selection of LP needles is important to Optimize patient care. Selecting a needle that is too short subjects the patient to unnecessary trauma with an excessive number of attempts and duration of the procedure. Selecting a needle that is too long increases the technical difficulty of the procedure because inserting short needles is easier than inserting long needles.
The Abe formula in this study appears to be more reliable for selecting needle lengths in comparison with previously published formulas. Because our data set is that used to derive this Abe formula, it is expected that the bbest Q formula would be derived to fit our set of data (the derivation data set). Thus, it cannot be assumed that our Abe formula is the best until it is validated by a separate data set (a validation data set).
A study that does not include many older children and adults will not be able to derive an accurate formula for the older children and adults. In general, for infants and children younger than 2 years, needle selection is more standardized because there is less body size variability (compared with teens and adults), resulting in less variability in the LP depth. Our Abe formula is based on a broader age distribution of patients (pediatric and adults, with infants
comprising b5% of the study group). Formulas that are derived from a cohort lacking obese study subjects will probably be less accurate for obese patients. Our Abe formula is based on a broad BMI study group. Body mass index distribution among the other 4 studies was not disclosed in the other 4 publications, but it is likely that the 2 studies dominated by infants [1,2] are not very likely to have a wide range of BMI values.
Using our study data, the Abe formula had the lowest number of needles that were too short, yet the Abe formula selected a needle that was too long 31% of the time. In examining the rates of selecting a needle that is too short, vs too long, there is a trade-off with no needle selection method being close to perfect in avoiding both too short and too long needles. However, it would be preferable to choose a needle that is too long rather than a needle that is too short. The other formulas frequently selected needles that were too short. In theory, this could be corrected by adding a constant (eg, 1 cm) to the formulas. This would reduce the formula’s rate of selecting a needle that is too short while increasing the formula’s rate of selecting a needle that is too long. Because the R2 values for the Abe formula and the formulas of Bonadio et al [1] and Hasan [3] were roughly similar, it is likely that once this correction is made to the formulas of Bonadio et al [1] and Hasan [3], their frequencies of selecting a needle that is too short would decline and they would probably be similar to the Abe formula. Because the formulas of Bonadio et al [1] and Hasan [3] were derived with predominantly small children, their constant might have been too small.
This study includes some limitations. (1) Heights and weights may not routinely be obtained in an ED (although they are not difficult to obtain). (2) And, the compatibility of CT measurements with the actual LP procedure may be questioned. One concern is that there is a difference in angulation of approach to the spinal column for an actual LP procedure in contrast to the perpendicular distance measured on CT. This small angulation or parallax error is likely negligible because the ratio of the 2 distances approaches
1.0 when the parallax error angle is small. Another concern for a CT measurement is that the soft tissue distance to the spinal canal for a patient in a flexed position might be less than that for a patient lying supine for a CT. Although flexing the spine will widen the spaces between spinous processes, it is unlikely that flexion will substantially decrease or increase the thickness of the Soft tissues and, hence, the distance from the skin to the spinal column. The supine position of the patient in a CT scanner could similarly affect the distance from the skin to the spinal canal. Another observation in the study was that, despite a considerable range of patient ages (1 month- 80 years) and sizes, there was relatively little variation in anterior- posterior spinal canal dimensions. The range of the spinal canal depth (distance from the anterior to the posterior aspect of the spinal canal) measured on CT was 1.0 to 2.6 cm
with a mean of 1.6 F 0.28 cm.
Our study did not include patients with musculoskeletal deformities, which can severely affect the ratio of weight to height more so than obesity alone. For example, patients with severe spinal deformities were not included in this study. This formula should not be extrapolated to such patients.
Considerations for future study include a validation data set of CT scans of varying body sizes to determine the accuracy of the Abe formula. Currently, clinicians select an LP needle length using current Clinical standards. Based on the data set of CT scan measurements in this study, these 4 published clinical standards [1-4] are likely to have a moderate degree of inaccuracy. Although not yet validated, application of the current Abe formula might be helpful, especially in obese patients, but the true utility of the Abe formula cannot be determined until further validation studies are completed.
In the clinical scenario described in the Introduction for a 110-kg, 166-cm man, an intern selected a 3.5-in needle. However, the Abe formula predicts a distance of 12.3 cm (4.8 in). Thus, a 5-in needle was used instead.
In conclusion, the depth to the spinal canal had a better correlation with patient weight-height ratio than with the individual variables of age, BSA, height, or weight that were used in other published studies. The Abe formula, LP
depth = 1 + 17 x (weight/height), might be a more reliable predictor for estimating the required LP needle length, but this must be validated by further studies. This formula resulted in significantly fewer estimates that were too short or too long for entry into the spinal canal of study subjects in comparison with other published formulas. This formula might be more useful for less experienced practitioners in selecting LP needles and/or when selecting an LP needle length for obese patients. It should be noted that none of the formulas were perfect. Selecting a needle that is too short occurs more frequently with obese patients. It is prudent to select a longer needle for an obese patient if the formula calculates a depth that is barely within the range of the needle at hand.
References
- Bonadio WA, Smith DS, Metrou M, Dewitz B. Estimating lumbar- puncture depth in children. N Engl J Med 1988;319(14):952 - 3.
- Craig F, Stroobant J, Winrow A, Davies H. Depth of insertion of a lumbar puncture needle. Arch Dis Child 1997;77(5):450.
- Hasan MA. Depth of epidural space in children. Anaesthesia 1994;49(12):1085 - 7.
- Henretig FM, King C, editors. Textbook of pediatric emergency procedures. Philadelphia7 Lippincott Williams & Wilkins; 1997.
p. 541 - 51.
